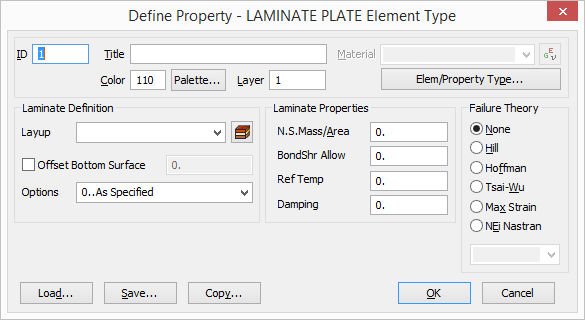
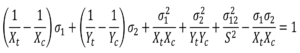Both the strength of bonds and laminates are important to understanding the whole story of composite failure in Femap with NX Nastran. This post will focus on using a 2D criterion to predict failure of laminates from element forces. In Femap, a failure theory will need to be chosen. There are actually a number of composite failure criteria as shown by the options under the laminate property definition menu:
Note the Failure Theory grouping to the right. Selectable options include one of the following:
- None
- Hill
- Hoffman
- Tsai-Wu
- Max Strain
- NEi Nastran
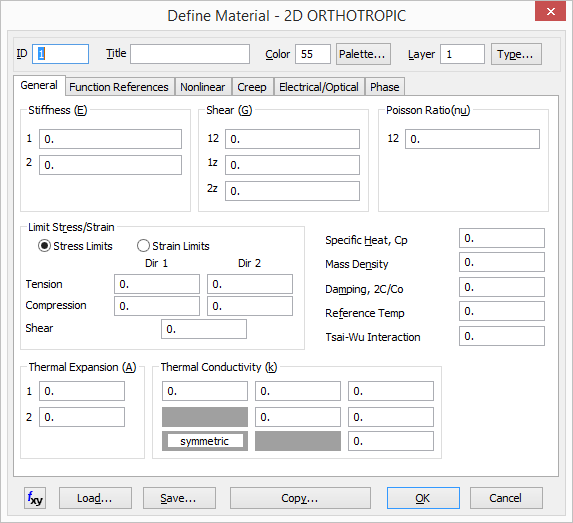
Additionally, material strength data must exist in the material definition under Limit Stress/Strain. These may be entered as stress or strain limits.
This example will just demonstrate how the Hoffman failure theory (criterion) can be used to determine whether or not a laminate will fail based on the results of a single element for simplicity. The Hoffman failure criterion looks like this:
There are stresses (σ1, σ2, and σ12), and strengths (Xt, Xc, Yt, Yc, S). When the left hand side of the equation equals or exceeds 1, failure is expected. Calculating the left hand side produces the failure index. The following calculator finds this failure index as well as strength ratio and margin of safety. Play around with the numerical inputs to gain an understanding of the relationship between strengths, stresses, failure index, and SR/ MS.
These values follow the example from Learning Femap. More information for introducing material data and options into the the previous Femap dialogs may be found in the Learning Femap book. If you or your company is interested in receiving training that covers composite failure analysis or how to implement in Femap/ NX Nastran, please see the training page.